Home » Blog » Covariance Matrix and the Matrix of Inertia
Covariance Matrix and the Matrix of Inertia
— Created: Xiaoke, 2017/07/24 17:08 CST
— Last modified: Xiaoke, 2017/07/31 09:51 CST
The main idea in this page is similar to the description of moment on wikipedia .
Covariance matrix is from statistics, and matrix (or tensor) of inertia is a concept in mechanics. Do they have anything in common?
From the definition of the covariance matrix of a random vector and the matrix of inertia of a 3D rigid body, my answer is that they actually refer to the same thing. The former characterises the distribution of a random vector, while the latter reflects the distribution of the mass of a rigid body in three-dimensional (3D) space. Moreover, for a 3D rigid body, the centre of mass corresponds the expectation of a random vector (first moment), and the matrix of inertia is equivallent to the random vector's covariance matrix (second moment).
As is known, the diagonal elements of a covariance matrix indicate the variance of the distribution ALONG each dimension. Correspondingly, the diagonal elements of a matrix of inertia specify the variance of the mass distribution AROUND each axis.
Since the off-diagonal element of a covariance matrix defines the covariance between two dimensions, i.e. how changes in one dimension are (linearly) associated to changes in another dimension. The off-diagonal elements of a matrix of inertia then specifies how the changes of the mass distribution in one dimension are associated to changes in another dimension. This may sound awkward, but look at figure below of a 2D distribution and the corresponding covaraince matrix. If an imaginary 2D rigid body has the same shape as the distribution, the off-diagonal elements of its matrix of inerita will have the same signs. The difference is that mass distribution is usually uniform, unless the density of the rigid body varies. Actually, the density of a rigid body is conceptually the same as the probability density of a distribution.
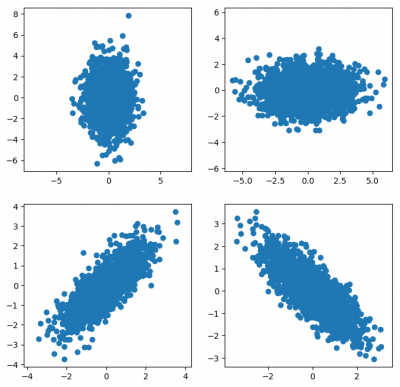 In the figure, the covariance matrices are [1 0;0 3](tl), [3 0;0 1](tr), [1 0.8; 0.8 1](bl), and [1 -0.8; -0.8 1](br).
In the figure, the covariance matrices are [1 0;0 3](tl), [3 0;0 1](tr), [1 0.8; 0.8 1](bl), and [1 -0.8; -0.8 1](br).
Basically, a 0 off-diagonal element in the matrix of inertia means that the shape of the rigid body is symmetric. A positive element indicates the rigid body lies largely along the positive directions of the two dimensions, while a negative element means that the rigid body lies largely along the positive direction of one dimension and the negative direction of another.